What Is The Size Of An Electron

In the year 1908, while the great minds of natural philosophy were puzzling over how to understand the structure of atoms in terms of the recently-discovered electron, Vladimir Lenin (yes,that Vladimir Lenin) declared that:

The electron is as inexhaustible as the cantlet

Lenin was making a philosophical point, but you can view his declaration as something similar a scientific prediction. Simply as scientists of his era were discovering that atoms were made from smaller constituents similar electrons, so too, he said, would we eventually find that the electron was made from even smaller components. And on the bicycle would become, with each new piece of matter beingness an "inexhaustible" source of new discovery.

It was a pretty reasonable expectation at the time, given the relentless progress of reductionist science. But so far, despite more than a century of work past scientists (including many presumably extra-motivated Soviets), we nevertheless have no indication that the electron is made from anything else, or that it has whatever internal structure. Students of physics in the 21st century are taught that the electron is a point in infinite with certain properties — mass, accuse, and spin — only that it cannot be idea of as a spinning sphere or anything else that has a size and shape. The electron looks pretty exhausted.

In this post, though, I want to take Lenin's side, and ask the heretical question: "If the electron really is a real, physical object with a finite size, then how big is it?" Non surprisingly, at that place is no clear reply to this question, but some of the candidate answers turn out to be pretty interesting.

Option #one: The Bohr radius

If you're a physicist, and someone asks yous "how large is an electron?", then the most canonically correct matter to say is "At that place is no concept of an electron size other than the spatial extent of the electron wavefunction. The size of the electron wavefunction is the electron size."

This opinion essentially amounts to telling someone that they need to stop trying to think nearly a quantum electron every bit a physical object that yous could hold in your hand like a baseball if only it was enlarged $10^{10}$ times. People who profess this stance are presumably besides the ones who get bellyaching by the popular proclamation that "matter is 99.999% empty space."

So, if such a person were pressed to give a numerical value for the "size of the electron", they might say something like "Well, nigh electrons in the universe are leap into atoms. And then the typical 'size' of an electron is about the same as the typical size of an cantlet."

As has been discussed here earlier, the typical size of an atom is given by the Bohr radius:

$a_B \sim 4 \pi \epsilon_0 \hbar^2/me^2$ .

[Here, $\hbar$ is Planck'due south constant, $\epsilon_0$ is the vacuum permittivity, and $m$ is the electron mass, and $e$ is the electron charge.]

Just to remind you how this length scale appears, you lot can figure out the rough size of an atom by remembering that an electron leap to an atom exists in a balance betwixt ii competing energies. First, there is the attractive potential energy $U \sim -e^2/4 \pi \epsilon_0 r$ that pulls the electron toward the nucleus, and that gets stronger every bit the electron size $r$ (which is about the aforementioned as the average distance between the electron and the nucleus) gets smaller. Second, there is the kinetic energy of the electron $KE \sim p^2/2m$ . The typical momentum of the electron gets larger as $r$ gets smaller, every bit dictated by the Heisenberg uncertainty principle, $p \sim \hbar/r$ , which ways that the electron kinetic energy getslarger as the atom size $r$ shrinks: $KE \sim \hbar^2/mr^2$ .

In the balanced state that is an atom, $PE$ and $KE$ are about the aforementioned, which means that $e^2/4 \pi \epsilon_0 r \sim \hbar^2/mr^2$ . Solve for $r$ , and yous get that the electron size is near equal to the Bohr radius, which numerically works out to about 1 Angstrom, or $10^{-10}$ m.

atom

So at present we take our showtime candidate answer to the question "how big is an electron?". If someone asks you this question, then you tin can sort of curlicue your optics and then say "normally, well-nigh $10^{-10}$ meters".

But permit'due south keep going, and see if there are whatever other concepts of an "electron size". Peradventure yous don't actually like the answer that "the size of the electron wavefunctionisthe electron size", considering the electron wavefunction tin can be different in unlike situations, which ways that this definition of "size" isn't really an immutable property of all electrons. Possibly you prefer to think about the electron as a tiny picayune brawl, and the wavefunction every bit a sort of probability distribution that describes where the brawl tends to be from time to fourth dimension. If you insist on this point of view, so what tin you say about the size of the brawl?

Option #two: The classical electron radius

If you lot're going to remember nigh the electron every bit a tiny charged ball, and so in that location is 1 thing that should bother you: that ball will have alot of energy.

To see why this is truthful, imagine the hypothetical process of assembling your tiny charged brawl from a bunch of smaller pieces, each with a fraction of the full charge. Since the pieces have an electrical repulsion from each other, and since you lot are bringing them very close to each other, the brawl will be very hard to put together.

sphere_puzzle

In fact, the energy required to "build" the electron is $E \sim e^2/4 \pi \epsilon_0 r$ , where $r$ is the electron size. So the smaller the electron is, the harder it is to build, and the more than energy gets stored in the form of electrical repulsion between all the pieces. The large self-energy of the electron also means that if the electron were to get "broken", so all the tiny pieces would fly apart from each other, and release a tremendous amount of energy.

Simply, in fact, by the end of the first decade of the 20th century, people already knew that a unmarried electron stored a lot of free energy. Einstein's famous equation, $E = mc^2$ , suggested that fifty-fifty a very pocket-size piece of affair was really an intensely concentrated course of free energy. One electron represents about $10^{-13}$ Joules (500,000 electron volts), which ways that it only takes a few cups' worth of electrons to have enough rest mass energy to equal the energy of an atomic bomb. (Of course, if y'all always actually removed all the electrons from a few cups' worth of affair, you would create something much worse than an atomic bomb.)

Then i of the early attempts to estimate a size for the electron was to equate these ii ideas. Perchance, the logic goes, the large "mass energy" of an electron is actually the same as the energy stored in the electric repulsion of its constituent pieces. Equating those two expressions for the free energy, $E = e^2/4\pi \epsilon_0 r = mc^2$ gives an estimate for $r$ that is called the "classical radius of the electron":

$r_c = e^2/(4 \pi \epsilon_0 m c^2) \sim 10^{-15}$ m

So that'southward our kickoff estimate for the intrinsic electron size: near $10^{-15}$ g.

This classical radius, past the way, works out to be most the same size as the typical size of an atomic nucleus. And this is, perhaps, where we become the typical middle schoolhouse movie of the atom: if you think about the electron using its classical radius, then the moving-picture show you get is of a tiny negatively-charged speck orbiting another equally tiny positively-charged speck, with about a factor $10^5$ departure between the speck sizes and the orbit sizes.

Option #3: The Compton Wavelength

This picture of the electron as a piddling charged ball with size $10^{-15}$ meters seemed relatively okay up until the 1920s, when information technology was discovered that the electron had more properties than just its charge and its mass. The electron besides has what nosotros at present phone call a "spin".

Basically, the concept of spin comes downward to the fact that the electron is magnetic: it has a north pole and a south pole, and it creates a magnetic field effectually itself that is every bit large as most 1 Tesla at a distance of 1 Angstrom abroad, and that decays in strength as $1/(\text{distance})^3$ . Another way of maxim this same thing is that the electron has a "magnetic moment" whose value is equal to the "Bohr magneton", $\mu_B = e \hbar/2m$ . (As it turns out, this magnetic moment is essentially the same equally the magnetic moment created by the orbit of an electron around a nucleus.)

At get-go sight, this magnetic-ness of the electron doesn't seem similar a problem. A charged sphere can create a magnetic field around itself, as long equally the sphere is spinning. Retrieve, for example, that electric currents create magnetic fields:

and that electric current is just moving electric charge. So a spinning charged sphere also creates magnetic fields past virtue of the move of its accuse-containing surface:

This sort of prototype is, in fact, why the electron's magnetic-ness was commencement called "spin". People imagined that the lilliputian electron was actually spinning.

A trouble arises with this flick pretty quickly, though. Namely, if the electron is very minor, then in order for it to create a noticeable magnetic field it has to be spinningreally speedily. In item, the magnetic moment of a spinning sphere with charge $e$ is something like $\mu \sim e \omega r^2$ , where $\omega$ is the sphere's rotation frequency. If the sphere is spinning very quickly, then $\omega$ is large, and the equator of the sphere is moving at a very fast speed $v \sim \omega r$ .

We know, notwithstanding, that nothing can move faster than the speed of lite (including, presumably, the waistline of an electron). This puts a limit on how fast the electron tin can spin, which translates to a limit on how small the radius of the electron can be if we have whatever hope of explaining the observed electron magnetic field in terms of a physical rotation.

In detail, if you set $\mu = e \omega r^2 = e v r = \mu_B$ , and crave that $v < c$ , and so y'all get that the size of the electron $r$ must be bigger than

$\lambda_c \sim \hbar/(m c) \approx 10^{-12}$ m.

In other words, if you hope to explicate the electron magnetic field as coming from an actual spinning motion, and so the size of the electron needs to exist at least $10^{-12}$ m. This is virtually a chiliad times larger than the classical electron radius.

Coincidentally, this value $\lambda_c$ is called the "Compton wavelength", and it has another of import meaning. The Compton wavelength is more or less the smallest distance to which y'all can confine an electron. If you endeavour to squeeze the electron into an even smaller distance, then its momentum volition go so large (via the uncertainty principle) that it its kinetic energy will be larger than $mc^2$ . In this case, at that place will be enough free energy to create (from the vacuum) a new electron-positron pair, and the newly-created positron tin just demolish the trapped electron while the newly-created electron flies away.

Option #four: the empiricist's view

At this bespeak you may outset to feel like none of the above estimates for the electron size seems meaningful. (Although don't be also harsh in discarding them: the concepts of the Bohr radius, the classical electron radius, and the Compton wavelength announced over and over again in physics.)

So let'southward consider a purely empirical view: what do experiments tell united states of america about how large an electron is?

I know of ii types of experiments that qualify equally saying something about the electron size. The kickoff is a measurement of the electric dipole moment of the electron. The thought is that, perhaps, the electron does not always have its charge bundled in a perfectly spherical way. Maybe its "shape" can be slightly asymmetric, similar this:

asymmetric_electron

An asymmetric electron

In this instance the electron would would want to align its "head" with an external electric field. The strength of the electron asymmetry is quantified past the electron dipole moment $d$ , which is defined equally something similar $d \sim ($ charge in the bottom half of the electron $-$ charge in the peak one-half of the electron $) \times ($ electron size).

So far, still, experiments looking for a finite value of the electron dipole moment have non establish one, and their experiments place an upper limit of $d < 10^{-30} \text{ electron charges} \times \text{meters}$ . This ways that either the electron is an extremely symmetric object (for example, a very perfect sphere) or its size is smaller than about $10^{-30}$ meters.

Another set of experiments looks for corrections to the mode that the electron interacts with the vacuum. At a very conceptual level, an electron can absorb and re-emit photons from the vacuum, and this slightly alters its magnetic moment in a way that is listen-bogglingly well-described. If the electron were to accept a finite size, then this would alter its interaction with the vacuum a fiddling bit, and the magnetic moment would very slightly change relative to our theories based on size-less electrons.

So far, however, experiments have seen no evidence of such an effect. The accuracy of the experimental observations places an apparent upper limit on the electron size of about $10^{-18}$ chiliad.

Option #five: The Planck length

At this point, seeing the apparent failure of the classical description to produce a coherent movie, and seeing the experimental appearance of such spectacularly small numbers every bit $10^{-18}$ and $10^{-30}$ , you lot may be willing to abandon Lenin'due south hope of an "inexhaustible" electron and but declare that the electron really is size-less. From at present on, yous may resolve, when you draw an electron, you'll draw information technology as a single pixel. Only only because you lot tin can't draw it as a half-pixel.

Merely this brings upwards the last, and strangest, question: what is the smallest believable length that anything can have? In other words, if the universe has a fundamental "pixel size", then what is information technology?

Of grade, I don't know the respond to this question. Whether there really is a "smallest possible length" is interesting to consider, merely at the moment information technology tin merely be addressed with speculation. Nonetheless, we do know that there is a length scale beneath which our most basic theories of the universe terminate making sense. This is chosen the "Planck length", $\ell_p$ . At distances smaller than the Planck length, nosotros are unable to describe even what empty infinite is like.

As I empathise it, the Planck length trouble can be viewed like this. Our modern agreement of the vacuum (i.e., of empty space) is that it contains i photon mode for every possible photon wavelength. This means that empty space is substantially total of photons of all conceivable energies and with all conceivable wavelengths.

Yet, photons with very small wavelength $\ell$ accept very large energy, $E \sim \hbar c/\ell$ . It should therefore exist possible to convert that energy, if only for a cursory instant, into a large mass $M = E/c^2$ . (Subsequently a short time $t \sim \hbar/E$ , the mass will have to disappear again and give its energy back to the vacuum). If that mass is large enough, though, it can create a small black hole. A black pigsty gobbles upwardly all other photons around information technology if they have a wavelength smaller than the black pigsty's Schwarzschild radius, $R_s \sim G M/c^2$ . (Here, $G$ is Newton's gravitational constant). This starts to exist a real problem when $R_s$ gets as large as the wavelength of the photon that commencement created the black pigsty, considering then the black hole can consume the original photon and all other photons with smaller wavelength.

Do you run across the trouble with that (semi-contorted) logical sequence? If very brusque length scales be, so very high energy photons exist. But if high energy photons exist, then they should exist able to create, for a brief moment, very loftier masses. Those loftier masses will create black holes. And those black holes will swallow up all the high energy photons.

It's sort of a logical inconsistency.

Every bit mentioned higher up, this problem first arises when the Schwarzschild radius $R_s$ becomes equal to the wavelength $\ell$ of the photon that created it. If you work through the chain of algebra to a higher place, this volition bring you to a length calibration of

$\ell_p = \sqrt{\hbar G/c^3} \approx 10^{-35}$ chiliad.

At any length scale smaller than $\ell_p$ , we don't know what'southward going on. At such small length scales either breakthrough theory should exist unlike from what we know, or photons should be dissimilar, or gravity should be unlike.

Or mayhap at such small length scales there is no proficient notion of continuous space at all. Such thinking, as I understand information technology, gives rise to lots of picturesque ideas about "breakthrough foam", and is the playground of (as yet mostly non-real) theories of quantum gravity.

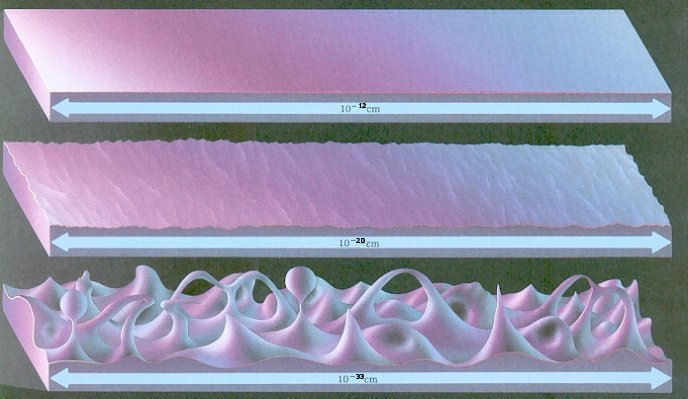
This picture is supposed to illustrate the idea that space might smooth and continuous until you try to look at it at the calibration of the Planck length.

What shall nosotros say most Lenin?

So in the end, was Lenin right about the electron being "inexhaustible"? For the moment, information technology looks like the answer is no, in the sense that there isn't really any serious candidate for the intrinsic size of the electron. In that sense, nosotros could all take saved some time by just accepting the standard dogma that an electron is a sizeless point in infinite.

But I personally tend to resist dogmatism in all its forms, even the kind that is almost certainly right. Because sometimes those heretical questions lead y'all through all sorts of interesting ideas, ranging from from $10^{-10}$ meters down to $10^{-35}$ meters.

And if it becomes clear some twenty-four hour period that Lenin's statement actually just works on the Planck scale, and then we can probably say that his prediction came several centuries earlier its time.